ECE 6605 - Information Theory

Prof. Matthieu Bloch

Tuesday, October 3, 2023

Announcements

Image
  • Assignment 1 and 2
    • Solutions posted on Canvas
    • Grading takes time…
  • Assignment 3
    • Coming up
  • Midterm
    • Moved to Tuesday October 17, 2023
    • In class, with notes (no electronic notes)
    • Covering essentially Hoemwork 1 & 2
  • Last time
    • A cool new result: Source coding with side information
  • Today
    • Privacy amplification
    • Glimpse of information theory and security
    • Applications to random number generation

Ultrafast random number generation

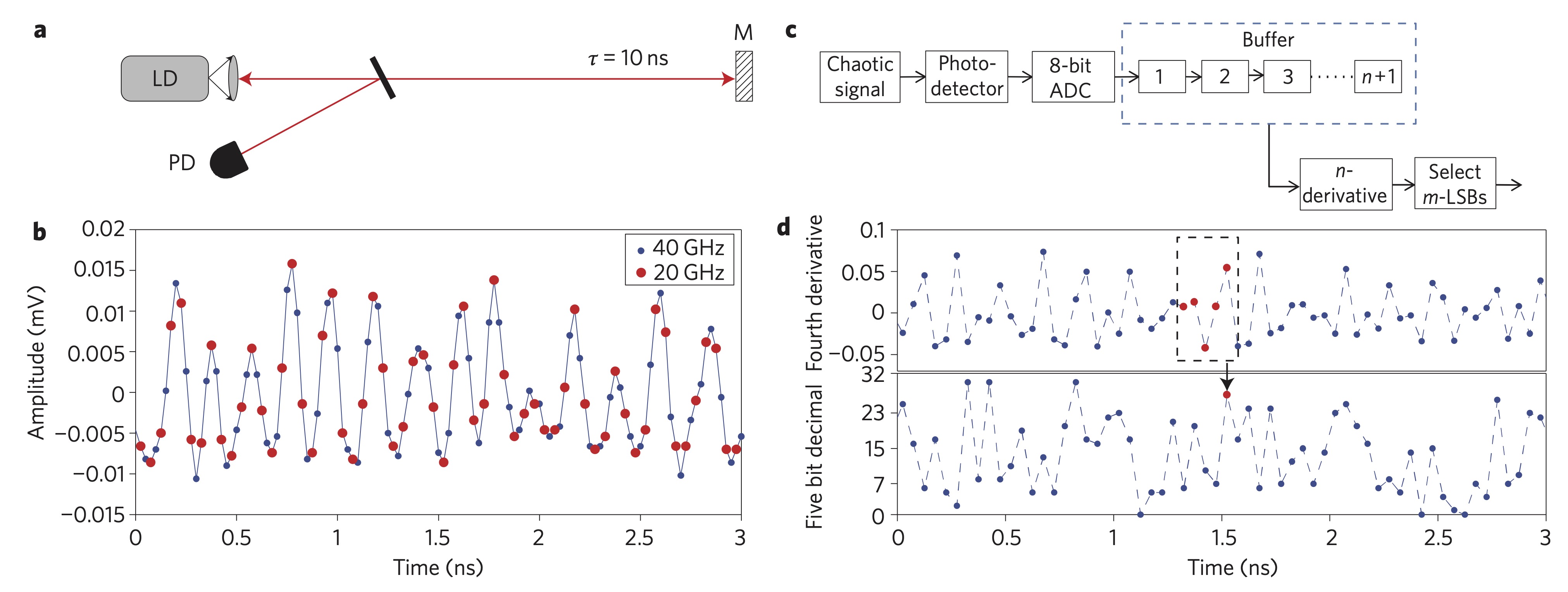
Image
(c) Nature Publishing Group
  • Ido Kanter et al., An optical ultrafast random bit generator, Nature Photonics, (2010)
    • The generation of random bit sequences based on non-deterministic physical mechanisms is of paramount importance for cryptography and secure communications.
    • We present a physical random bit generator, based on a chaotic semiconductor laser, having time-delayed self-feedback, which operates reliably at rates up to 300 Gbit/s.
    • The randomness of long bit strings is verified by standard statistical tests.
  • Chaotic laser intensity fluctuations digitized at a 20 GHz sampling rate with an 8-bit resolution
    • How much true randomness can we generate?

Privacy amplification

Image
Privacy amplification model

A \((n,K_n)\) code \(\calC\) for privacy amplification coding a discrete memoryless source \(p_X\) against side information \(Z\) consists of an encoding function \(f_n:\calX^n\to\set{1;K_n}\).

  • The performance of an \((n,K_n)\) code is measured in terms of

    1. The rate of the code \(R\eqdef \frac{\log_2 K_n}{n}\) (bits/source symbol)

    2. The secrecy and uniformity of \(M\) measured as

      \[\begin{align*} S^{(n)}(\calC) \eqdef \bbV(P_{MZ^n},Q_M\cdot P_Z^{\otimes n}) \end{align*}\]

      where \(Q_M\) is the uniform distribution on \(\set{1;K_n}\)

Privacy amplification

  • Define again \[ C_{\textsf{pa}}\eqdef \inf\left\{R: \exists \set{f_n}_{n\geq 1} \textsf{ with }\lim_{n\to\infty}\frac{\log K_n}{n}\geq R \text{ and } \lim_{n\to\infty}S^{(n)}=0\right\} \]

For a discrete memoryless source \(P_{XZ}\), \(C_{\textsf{pa}} = \bbH(X|Z)\)

Achievability

  • Consider a generic source \((\calV,P_V)\) and a generic channel \((\calV,W_{U|V},\calU)\) with \(\card{\calU}<\infty\).

  • For \(\gamma>0\), let

    \[\begin{align*} \calD_\gamma=\left\{(u,v)\in\calU\times\calV:\log\frac{1}{P_{U|V}(u|v)}>\gamma\right\}. \end{align*}\]

  • For each \({u}\in\calU\), let \(f({u})\) be a bin index drawn independently with uniform distribution on \(\intseq{1}{K}\).

  • Define an encoder as the mapping \({u}\rightarrow f({u})\).

For any \(\gamma>0\),

\[\begin{align*} \E{\bbV(P_{VK},P_{V}Q_K)} \leq \P[P_VW_{U|V}]{(U,V)\notin \calD_\gamma} + \frac{1}{2}\sqrt{\frac{K}{2^{\gamma}}}. \end{align*}\]

Converse

Consider a sequence of codes \(\set{f_n}_{n\geq 1}\) such that \(\lim_{n\to\infty}S^{(n)}=0\) and \(\lim_{n\to\infty}\frac{\log K_n}{n}\geq R\). Then \(R\geq \bbH(X|Z)\)

  • We shall use a supporting lemma

For \(P,Q\in\Delta(\calX)\), we have \[ \abs{H(P)-H(Q)} \leq \bbV(P,Q)\log \frac{\card{\calX}}{\bbV(P,Q)} \]